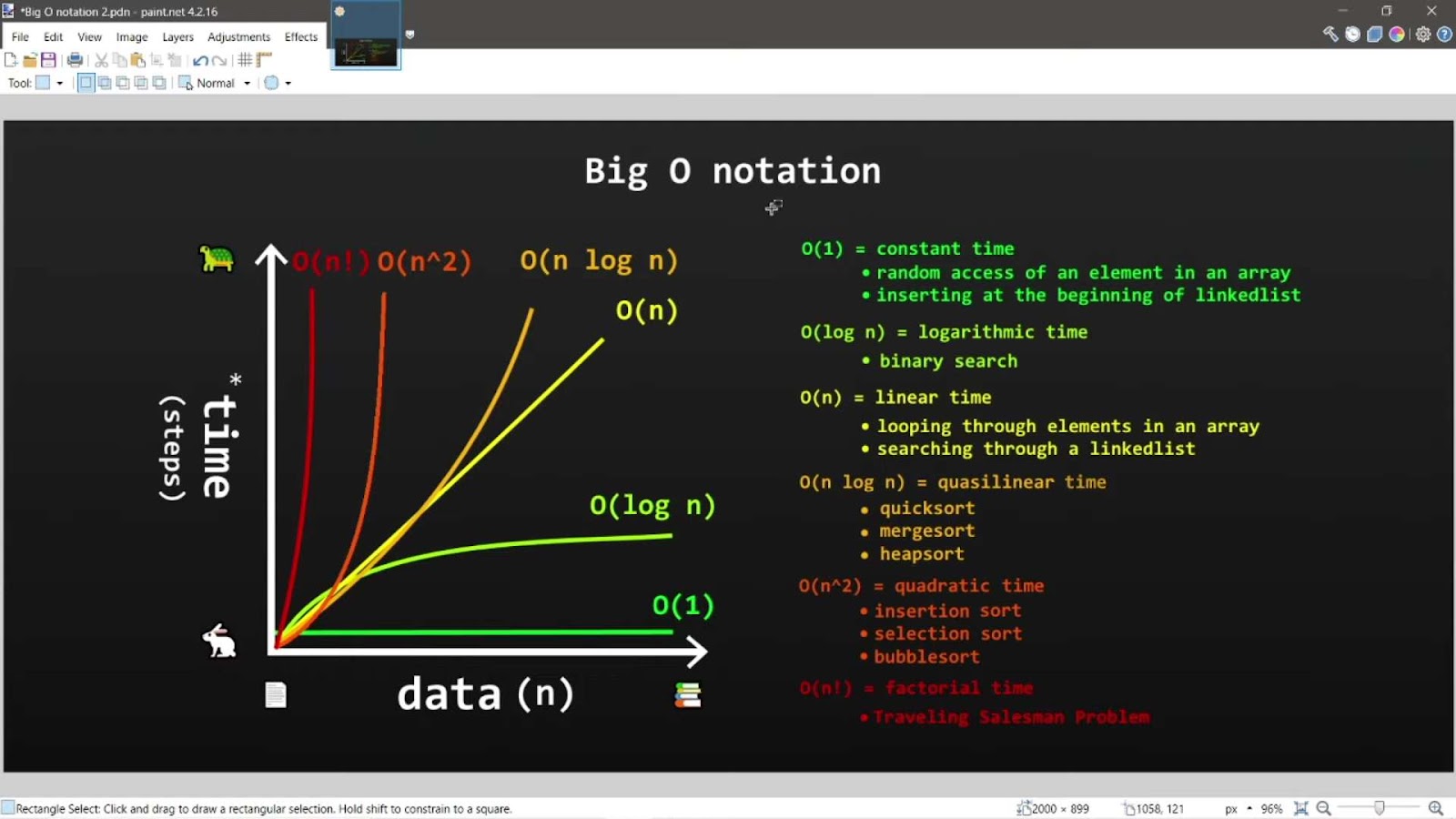
Demystifying the Big O Notation Chart
Big-O notation serves as a means to encapsulate the utmost complexity scenario of an algorithm. By harnessing algebraic expressions, it articulates the intricacy inherent in an algorithm, thereby affording you the capability to gauge its effectiveness and operational prowess.
In simple terms, the notation O(1) denotes constant time complexity, representing the pinnacle of efficiency, whereas O(n!) signifies factorial time complexity, a significantly less efficient scenario. The variable ‘n’ within these complexity expressions denotes the input size, signifying that O(n) implies that the algorithm’s time complexity will increase linearly in direct proportion to the input size.
Beyond the realm of Big-O notation, various other notations serve to elucidate an algorithm’s complexity. These include Ω (Omega) and Θ (Theta), each with its distinctive purpose. Ω elucidates an algorithm’s best-case complexity, portraying the most favorable scenario. On the other hand, Θ unveils an algorithm’s average-case complexity, providing insight into its typical performance characteristics.
Comprehensive Guide to Time Complexities of Key Data Structures
Time complexity is an essential factor in evaluating the efficiency of an algorithm or a data structure. It essentially indicates the amount of time an operation takes concerning the number of elements in the structure. While many data structures might appear to perform similarly, their underlying time complexities can greatly differ. This guide delves deeper into the average time complexities of several pivotal data structures prevalent in web development.
Average Time Complexities of Popular Data Structures
| Data Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | Θ(1) | Θ(n) | Θ(n) | Θ(n) |
| Queue | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Stack | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Doubly Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) |
| Skip List | Θ(log n) | Θ(log n) | Θ(log n) | Θ(log n) |
| Hash Table | N/A | Θ(1) | Θ(1) | Θ(1) |
| Binary Search Tree | Θ(log n) | Θ(log n) | Θ(log n) | Θ(log n) |
Understanding Time Complexities of Data Structures
| Data Structure | Access Complexity | Search Complexity | Insertion Complexity | Deletion Complexity |
|---|---|---|---|---|
| Array | O(1) – Constant time as direct indexing is possible. | O(n) – Linear time since it may need to traverse the entire array in the worst-case scenario. | O(n) – Elements might need shifting. | O(n) – Like insertion, shifting might be needed after deleting an element. |
| Queue | O(n) – Traversal might be required to access a specific element. | O(n) – Worst-case scenario requires full traversal. | O(1) – Typically, insertion happens at the rear end. | O(1) – Deletion usually happens from the front. |
| Stack | O(n) – To access a specific element, one might need to traverse through other elements. | O(n) – A full traversal might be needed. | O(1) – Push operation is typically constant time. | O(1) – Pop operation is constant. |
| Linked List | O(n) – One has to traverse sequentially to access a specific node. | O(n) – Similar to access, full traversal might be required. | O(1) – While adding at the beginning is constant, adding in between or end depends on the scenario. | O(1) – Given the reference to the node, deletion is constant time. |
| Doubly Linked List | O(n) – Both forwards and backward traversal might be needed. | O(n) – Worst-case scenario demands full traversal. | O(1) – Insertion can be efficient with pointers from both sides. | O(1) – Efficient deletion due to pointers from both directions. |
| Skip List | O(n) – Linear traversal in a worst-case scenario. | O(n) – Full traversal is sometimes necessary. | O(n) – Requires rearrangement of pointers. | O(n) – Deletion might demand reconfiguring the list. |
| Hash Table | N/A – Direct addressing is typically used. | O(n) – In cases of collisions and a poor hashing mechanism. | O(n) – Resolving collisions might need extra time. | O(n) – Deletion could be complex if collisions are present. |
| Binary Search Tree | O(n) – For skewed trees, traversal is linear. | O(n) – Worst-case is when the tree is not balanced. | O(n) – Insertion can take linear time in skewed trees. | O(n) – Deletion, especially with two children, can be complex. |
Analyzing Time Complexities of Array Sorting Algorithms
| Algorithm | Best Time | Average Time | Worst Time | Comments |
|---|---|---|---|---|
| Quick sort | Ω(n log n) | Θ(n log n) | O(n^2) | Highly efficient on average but can degrade in certain scenarios. |
| Merge sort | Ω(n log n) | Θ(n log n) | O(n log n) | Offers consistent performance but might require additional space. |
| Heap sort | Ω(n log n) | Θ(n log n) | O(n log n) | Memory efficient and consistent, suitable for large datasets. |
| Bubble sort | Ω(n) | Θ(n^2) | O(n^2) | Simple but less efficient for larger lists. |
| Insertion sort | Ω(n) | Θ(n^2) | O(n^2) | Efficient for small lists or nearly sorted lists. |
| Selection sort | Ω(n^2) | Θ(n^2) | O(n^2) | Simple to understand but not the most efficient. |
| Bucket sort | Ω(n+k) | Θ(n+k) | O(n^2) | Best for uniformly distributed data and requires additional space. |
In summary, understanding these time complexities provides a roadmap to select the right algorithm or data structure for specific requirements. Considerations such as available memory, the expected size of the dataset, and the nature of operations play a critical role in making these choices.
Insightful Notes on the Data Structures
- Array: Arrays provide constant time access to any element given its index. However, since elements in an array are contiguous, inserting or deleting an element requires shifting other elements, leading to a linear time complexity for these operations;
- Queue: A queue generally uses an array or linked list underneath. While inserting (enqueue) and deleting (dequeue) operations are usually constant, accessing or searching elements takes linear time due to the FIFO (First-In, First-Out) nature;
- Stack: Like a queue, a stack also typically uses an array or linked list. Operations such as push (insert) or pop (delete) are constant time. However, access and search are linear since it works on the LIFO (Last-In, First-Out) principle;
- Linked List: One of the main advantages of linked lists is their ability to insert or delete nodes in constant time, assuming the node reference is already available. Access and search operations require traversal, thus taking linear time;
- Doubly Linked List: Similar to the regular linked list, but with nodes pointing both forward and backward, ensuring constant time insertions and deletions. The bidirectional pointers do not improve search or access times, which remain linear;
- Skip List: It’s a layered linked list that allows for faster search operations compared to the regular linked list by skipping over a fixed number of elements, leading to logarithmic time complexities;
- Hash Table: A hash table, or hash map, provides almost constant time for search, insertion, and deletion operations due to the underlying hashing mechanism. However, direct access by index isn’t a typical operation, hence marked as N/A;
- Binary Search Tree (BST): A balanced BST ensures logarithmic time complexities for access, search, insertion, and deletion due to its hierarchical structure. However, if the tree becomes skewed or unbalanced, the time complexity can degrade to linear.
Conclusion
By understanding these time complexities, developers can make informed decisions when selecting the appropriate data structure for their specific use cases, optimizing performance and resource usage.
Mastering Array Cleansing in JavaScript
Big-O notation serves as a means to encapsulate the utmost complexity scenario of an algorithm. By harnessing algebraic expressions, it articulates the intricacy inherent in an algorithm, thereby affording you the capability to gauge its effectiveness and operational prowess. In simple terms, the notation O(1) denotes constant time complexity, representing the pinnacle of efficiency, whereas …
Exploring JavaScript’s Power in Managing URLs
Big-O notation serves as a means to encapsulate the utmost complexity scenario of an algorithm. By harnessing algebraic expressions, it articulates the intricacy inherent in an algorithm, thereby affording you the capability to gauge its effectiveness and operational prowess. In simple terms, the notation O(1) denotes constant time complexity, representing the pinnacle of efficiency, whereas …